こんにちは、今回は整式の除法について書きたいと思います。
タイトルにあるように、基本から応用までやっていきたいと思います。
整式の除法とは?
整式の除法とは、多項式を多項式で割ることです。
といってもわかりにくいと思うので具体例を挙げたいと思います。
(x²+3x+2)÷(x+1)
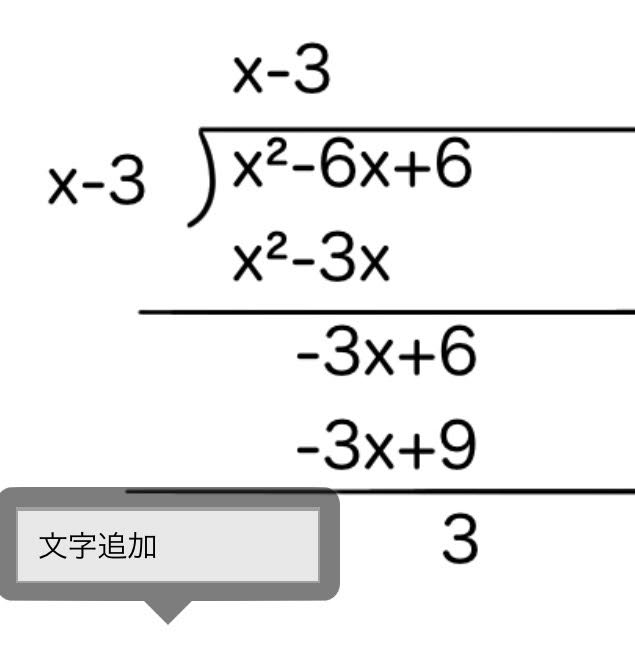
(x²−6x+6)÷(x-3)
などです。
これらの商を求めるために、筆算をします。
このようになります。
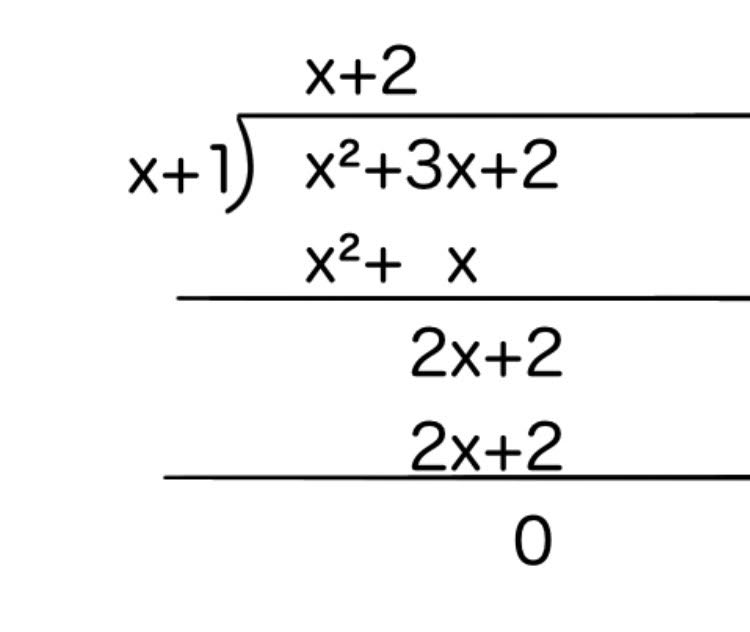
整式Aを0でない数式Bで割ったときの商をQ、余りをRとすると
A=BQ+R B>R
となります。
上の例をそれぞれ代入してみると
x²+3x+2=(x+1)(x+2)+0
x²-6x+6=(x-3)(x-3)+3
です。
AとBが与えられている状態です。
問題によっては余りと商、整式Aが与えられていてBを求めるということもあるでしょう。
2種類の文字がある場合
次は2種類の文字がある場合です。
文字が2種類以上ある場合はどの文字について解くのかが問題文中に書いてあります。
以下の問題はxについて考えます。
問1 (x²−6xy+6y²)÷(x-3y)
問2 {2x²-(y+3)x+(-y²+3y-1)}÷(2x-3y+1)
などです。
問1に関しては、文字が1種類のときと同じように解けるとおもいます。
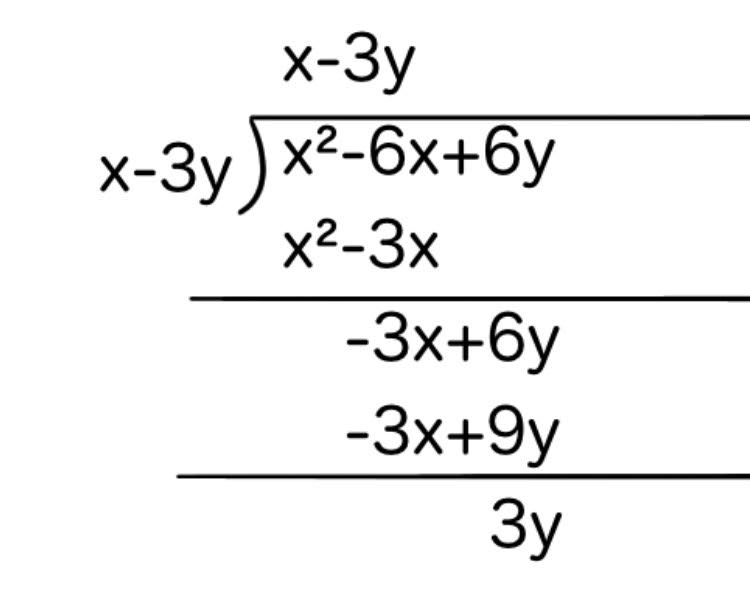
難しいのは問2です。
この問題で大切なことは、項にxを含まない数や文字をまとめることです。
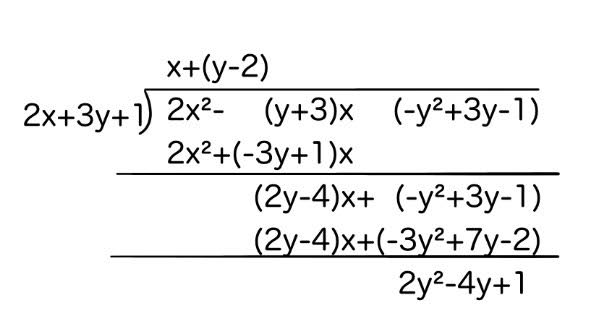
xの項を展開せずにそのまま計算します。
(2y-4)x=(y-2)2x
となり(y-2)が商に立ちます。
3種類の文字がある場合
3種類の文字を含む場合は2種類のときの問2と同じように解けます。
{2x²-(y+3z)x+(-y²+3yz-z²)}÷(2x-3yz+z²)
です。
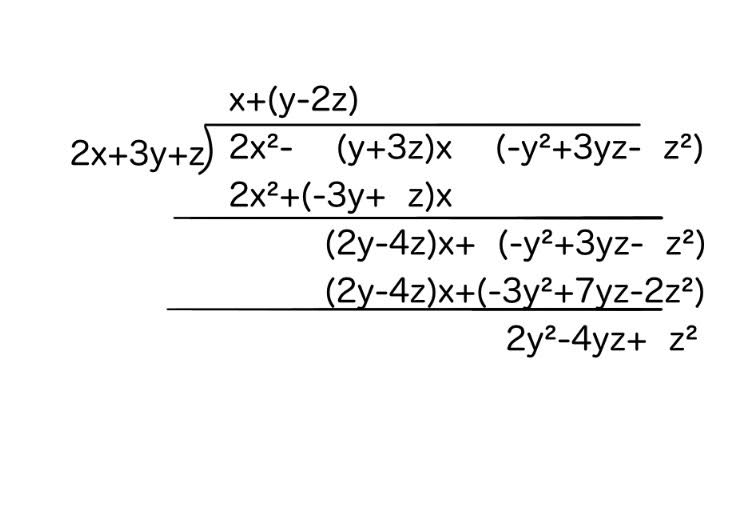
xでそれぞれをくくって整理してあげれば、これらの問題は解くことができると思います。
まとめ
今回は整式の除法について解説しました。
テストでいろいろな形に変えて出題すると思いますが、基礎を固めればどんな問題も解けると思います。
これは余談ですが、筆算を書くのがとても面倒でした。
手書きは、私の「字が汚くて読めない、、」となったらイヤなので頑張って打ちました笑
最後まで読んで頂きありがとうございました。


コメント